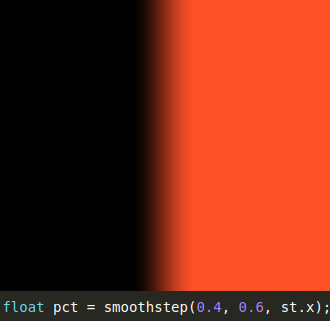
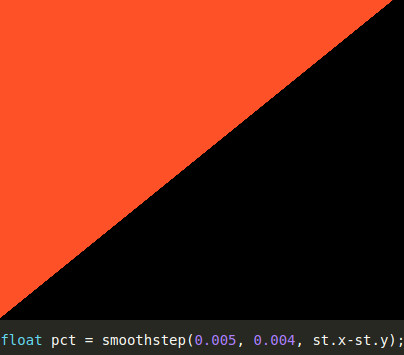
 |
 |
 |
  |  |
|||
| t1 = 0.4 en t2 = 0.6 dus t1 < t2 | t1 = 0.6 en t2 = 0.2 dus t1 > t2 |
De smoothstep functie terug naar de inleiding zie The Book of Shaders hoofdstuk 5
Omdat in shaders de overgangen van wit naar zwart scherp zijn zie je een karteling. De pixels zijn zwart of wit.
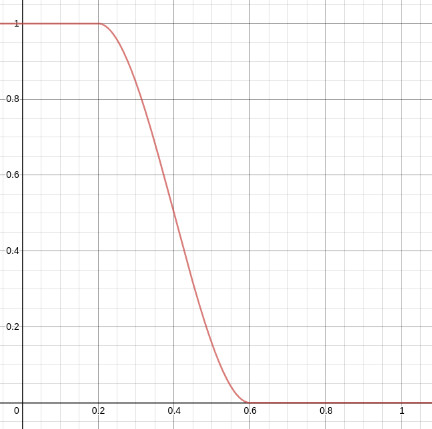
De karteling verdwijnt als er op die rand wat grijze pixels komen. Dit wordt gerealiseerd met de smoothstep curve.
De smoothstep curve heeft 3 argumenten
smoothstep(t1, t2, de x waarde van een punt op de curve);
t1 = de eerste drempel op de curve
t2 = de tweede drempel op de cuve
als t1 lager is dan t2 gaat de curve van 0 naar 1, dus het schuine deel is stijgend.
als t1 hoger is dan t2 gaat de curve van 1 naar 0, dus het schuine deel is dalend.
afstand tussen t1 en t2
een zeer stijle dus smalle curve geeft nog een gekartelde lijn. bijvoorbeeld bij een afstand tussen t1 en t2 van 0.001
een zeer brede curve geeft een vage lijn. bijvoorbeeld bij een afstand tussen t1 en t2 van 0.2
een niet vage lijn zonder karteling bij een curve met bijvoorbeeld bij een afstand tussen t1 en t2 van 0.01 of 0.04
zie regel 31 met een gekromde lijn. De lijn wordt getekend als de waarden abs(st.x*st.x-st.y) tussen de 0.004 en 0.005
want dit zijn de waarden in het stijgende deel van de curve. voor alle waarden buiten dit interval is abs(st.x*st.x-st.y) negatief en zal pct 1 zijn
#ifdef GL_ES
precision mediump float;
#endif
uniform vec2 u_resolution;
void main() {
vec2 st = gl_FragCoord.xy/u_resolution;
// voorbeelden hierin is t1 < t2 dus de curve gaan van 0 naar 1
// float pct = smoothstep(0.4, 0.6, 0.1); // punt op de curve is lager dan de lage drempel, ptc = 0 color, colorvector = 0, canvas is zwart
// float pct = smoothstep(0.4, 0.6, 0.5); // punt in het midden van het schuine deel, pct = 0.5 de kleur is vervaagd
// float pct = smoothstep(0.4, 0.6, 0.6); // punt op hoge drempel pct = 1, de colorvector heeft de ingestelde kleur
// nu punten op de curve van de genormaliseerde st.x en st.y, met waarden tussen [0.0, 1.0]
// float pct = smoothstep(0.4, 0.6, st.x); // breed overgangsgebied in het midden van het canvas
// float pct = smoothstep(0.004, 0.005, st.x-st.y); // smal overgangsgebied met schuine overgang van zwart naar kleur
// float pct = smoothstep(0.005, 0.004, st.x-st.y); // smal overgangsgebied met schuine overgang van kleur naar zwart, t1 > t2
// nu smoothstep met de abs() functie
// float pct = smoothstep(0.04, 0.05, abs(st.x-st.y)); // schuine zwarte lijn in een gekleurd vlak.
// float pct = smoothstep(0.05, 0.04, abs(st.x-st.y)); // schuine gekleurde lijn in een zwart vlak, t1 > t2
// nu smoothstep met st.x*st.x
// float pct = smoothstep(0.004, 0.005, abs(st.x*st.x-st.y)); // parabolisch gekromde lijn met gekleurde achtergrond, t1 < t2
float pct = smoothstep(0.005, 0.004, abs(st.x*st.x-st.y)); // parabolisch gekromde lijn met zwarte achtergrond, t1 > t2
vec3 color = pct*vec3(1.000,0.316,0.153);
gl_FragColor = vec4(color,1.0);
}
 |
 |
 |
|||
| t1 > t2, als st.x - st.y negatief is wordt pct = 0 |
t1 < t2, door st.x*st.y - st.y
wordt de lijn naar beneden gedrukt |
t1 > t2, door st.x*st.y - st.y
wordt de lijn naar beneden gedrukt
|